PACKTEXT
TEXT COMPRESSION AND HUFFMAN CODING
WITH PERSONAL PASCAL
by Daniel Matejka
A completely GEM based compression program for compacting text files; includes a lucid introduction to information theory, Huffman encoding, the ASCII character set, and tree structures. You can find the compression program and the voluminously commented source code on your START disk.
File PACKTEXT.ARC on your START disk
In the 1940's, Claude E. Shannon of the Bell Technical laboratories devised a set of theorems which sprouted a new branch of science called information theory.Shannon's work showed, among other things, that many messages are redundant;they contain more information than is really needed. Once redundant patterns are recognized, they can be encoded more efficiently.
PACKTEXT is a file compressor and decompressor. It strives to remove much of the redundancy within a text file. It can pack large files into considerably less space without loss of data. It will also, handily, read its own packed files and return them to their original form. While designed specifically for use with ASCII text, it will work on any data, though it may actually create larger files.
This technique is widely useful and can be directly incorporated into other applications. For example, a RAM-based database could use packed data, unpacking only one record at a time for display or processing, and expand its capacity by perhaps 40% before tackling the complications of going to a disk-based system. This technique could also be the basis for a data encryption scheme since it isn't immediately obvious what the original text looked like.
THE CONCEPT
Most micros use the ASCII character set to save, transmit, and otherwise manipulate text. The standard ASCII set contains 95 unique characters: 26 uppercase letters, 26 lowercase, 10 digits, the space, plus 32 punctuation marks and other symbols of dubious usefulness. The computer represents each character as a unique binary code, and 95 distinct symbols of any type require at least seven bits to encode (26< 95 <=27). Notice that the only correlation between any seven bit code and the character it is intended to represent is a matter of interpretation. A pattern of seven bits could just as easily be the beginning of a color palette, part of a DEGAS picture, or just random gibberish. The whole idea behind ASCII was to invent 95 different bit patterns, assign some meaning to each, and attempt to make the whole thing appear as if it were conceived by a guiding intelligence.
The Atari ST is constructed so the smallest addressable unit of memory is the byte: eight consecutive bits. If you only want seven bits, you'll have to access the whole byte and pick out the ones of actual interest once they're all inside the CPU.
Since the smallest convenient chunk of addressable memory (eight bits) is only barely larger than the smallest chunk necessary to encode an individual ASCII character (seven bits), it makes sense to represent a character with eight bits instead of seven. Eight bits allow 28=256 distinct patterns to be represented, so 256 different characters are representable in such a character set. The standard ASCII set defines the first 7 bits worth: the 95 so-called "printable" characters plus 33 control characters (whose exact meaning is often questionable) for a total of 128. Since we have an unused bit, many computers define an additional 128 of their own to fill out the remaining space.
In a text file, for example, each separate character is encoded by the ASCII pattern lurking in a byte of memory somewhere--one pattern to a byte. The hardware and software that scans memory, finds a byte of some value, recognizes it as printable character, and then rearranges the pixels on the screen to look like that character, is something else entirely. It is only a matter of convention that the bit pattern "01100101" looks like an "e" on a screen or printer.
MAKING IT SMALLER
Compression depends on finding a more space-efficient method of representing data. Different techniques work on different types of data. If it's ASCII text compression, we want to find some sort of encoding method in which, on the whole, less than eight bits are required to represent each individual character. There's nothing really sacred about "01100101," after all.
If you were to analyze a large body of text (this magazine, for example) a pattern would emerge. Some letters appear more often than others, and some might not appear at all. In the English language, the letter "e" is the most common. Generally, about 13% of all letters in a "typical" English text will be "e." "e" is followed in frequency of use by "t," at about 10%, "a," at about 8%, and then about 23 others, down to "z," at less than 0.1%. PACKTEXT takes advantage of this frequency distribution.
As mentioned before, in ASCII text files, all characters are encoded as a sequence of eight bits. This is just a function of the design of the character set, and a matter of convenience. If fewer than eight bits were used per character, the result would of course be a shortened file. In fact, since the "printable" ASCII characters are all contained within the first 128 members of the set, a "printable" ASCII file can immediately be shortened 12% by simply lopping off the high bit and packing the remaining seven together.
HOFFMAN CODES
Consider a system using fewer than eight and even fewer than seven bits to represent each of the characters of the ASCII set. Only an unforgivably small subset of the ASCII set can be contained in a scheme using only three or four bits per character, but consider a system in which not all characters use the same number of bits, where some are represented by as few as three or four, and others by as many as 14 or 15.
Huffman Codesuse the smallest number of bits practical for commonly occurring characters and necessarily more bits for the less common ones. These unevenly sized codes can then be glommed together, disregarding simple matters of convenience like bit boundaries.
How can we determine how many bits to use for each character? And, how can we construct the table of packing codes so that it will be clear where the border lies between separate characters? Both problems are nontrivial. If we can accomplish them, and the text to be compressed cooperates by being something more than purely random gibberish, as often happens with useful information, a practical data compression scheme emerges.
The second problem is the easier of the two. In fact, it may be trivial. The delineation of codes is accomplished by constructing the table so that no packing code begins with a sequence of bits that is the same as a shorter-code. For example, if the code for "e," the most common letter and therefore the owner of the shortest code, is three bits, say "000," then no code for any other letter can begin with the same sequence "000." Other, longer codes can containthat sequence, but to ensure each unique character has a unique recognizable pattern in the packed bit stream, none can begin with it.
If "t," for example, was encoded as "0001," it would be unclear if that pattern meant "t", or "e" followed by the beginning of something else. Perhaps the decoding algorithm could be clever enough to know the difference. PACKTEXT certainly isn't. However, if "t" was encoded as "10001," even though it contains the sequence "000" (which could mean "e"), by the time the decoding algorithm gets that far it should realize it isn't an "e." All we need to know is where the character begins in the packed bitstream and that the opening sequence of each character is unique.
| FIGURE 1 | |||
|
This is where the trick in determining just how many bits to use for each packing code comes in. If "e" is encoded as just mentioned, then all the other seven possible combinations of three bits are available as starting sequences for other characters. If less common characters are encoded with more bits and don't begin with the sequence "000," then additional characters can be accommodated. If instead the next most common character, probably "t," is also encoded in three bits, perhaps "001," then, even if the jump to four bits is made immediately afterward, we are only left with room for twelve more unique starting codes (0100-1111). The trick is to determine the optimum length for the shortest packing code, and when to make the jump to longer codes for subsequent less common characters. Our hope is that the more common characters are common enough so that the less common ones (which will no doubt require more than the original eight bits to represent), won't weigh down the entire scheme and actually produce a longer packed file.
A well-constructed Huffman Code for "typical English text," consisting of all capital letters and nothing else, will require an average of about 4 bits per character, thereby shortening the entire text file by nearly 50%. A similarly well-constructed code for text such as this article which includes characters of both upper case, lower case, and punctuation marks, will require about 5 bits per character: a 35% savings. "Average bits per character" refers to the length of each character code weighted by its frequency of use; it is indicative of the total length of a packed text file. Specifically, it is the sum of the products of the normalized frequency of occurrence of each character and its corresponding code length.
A CLOSER LOOK
As an example of a Huffman Code, an analysis of an early version of this article yielded the table of packing codes in Figure 1,truncated at the point where Frequency of Occurrence drops below 1%. Packing efficiency was better than 40%, with the average character requiring about 4.5 bits to encode.
Two things jump out from this table. First, carriage returns apparently outnumber linefeeds. This I attribute to roundoff error. Second, the Huffman Codes illustrate that no code begins with a bit sequence which duplicates a shorter code.
GENERATING UNIQUE CODES
If, before constructing the actual codes, the desired length of each code is already known, and the table is constructed in order from shortest code to longest, then each code is just the previous code + 1, shifted left if it is longer. "e," for instance, is "010." The next character, "t" is "e" + 1, or "011." The next character, "s," is "t" + 1, or "100," except that at this point we want to begin using five bits instead of three, so enough zeroes are tacked on to the end to make up the difference with "10000." The first n bits in a code, where n is the number of bits used by the immediately preceding code (and is less than or equal to the number of bits in the current code) must be unique. The following bits, if any, can be anything at all, but zeroes are always used here because that allows the simple operation of adding 1 to get the subsequent code.
We need not begin with 0; we could instead begin at the other end with 2, -1, or anywhere in between. The problem with beginning anywhere in between is just remembering which patterns have already been used, and not reuse them while casting about for the next unique sequence. If we begin at one of the ends, then the simple task of incrementing (or decementing) by one each time guarantees a unique pattern.
With such a scheme, as long as the addition of 1 to the previous code never causes a carry, or overflow,into more bits than were expected, then no code will ever have another shorter code as its opening sequence. An overflow occurs when n bits, all 1's, are incremented. The result is a 1 followed by n 0's, which contains as its opening sequence a bit pattern already used. The bottleneck in this process is actually determining how long each code should be; where to jump to a longer code early enough to prevent pattern repetition (overflow) but late enough to avoid an unnecessarily long average code length.
DETERMINING OPTIMUM CODE LENGTH
Directly stated, the optimum number of bits b necessary to encode a character with a normalized probability of occurrence p is given by:
b= -log2 p
As an example, the table we looked at earlier shows that the most common character, the blank, makes up 17.9% of the file. It would optimally be encoded, then, with -log2 0.179=2.5 bits. Because rounding down would cause the overflow problem mentioned above, we can round up instead to get blank encoded in 3 bits. Notice, however, that in the above table it is actually encoded in 2 bits. PACKTEXT determines the length of each code should be by starting with ceil(-log2 p) bits as an approximation, then attempts to use less and see how much can be gotten away with. A dash of brute force always helps any recipe.
I won't attempt to derive the formula for b because I'm not certain I can. Rather, I present a few scenarios designed to make it more palatable. Consider a case in which only eight characters need to be packed, and they all occur with equal frequency. Each character would have a normalized probability of occurrence of 12.5%, so each character should be encoded with —log2 0.125=exactly three bits. Funny that exactly eight combinations are available using exactly three bits. Drop a few probabilities, thereby increasing some others, and the equation moves around in a suitably accommodating direction.
If only seven characters of all equal probability were being packed, the formula suggests 2.81 bits apiece 22.81=7. Too bad. We must use an integral number of bits, so PACKTEXT would begin with all seven using three bits, then drop the first one to two just because it can.
UNPACKING
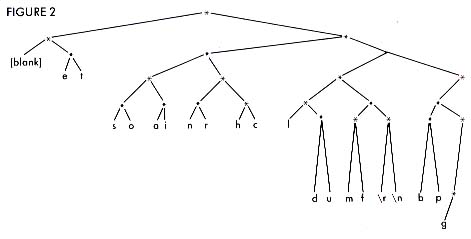
The only remaining problem is inventing a decent algorithm for unpacking the packed text. PACKTEXT traverses a binary tree to accomplish this feat. Figure 2shows an unpack tree corresponding to the table in Figure 1.
To traverse this tree and find the surprise character at the end, begin with the root node and the most significant bit. At each node take the left branch for a 0 and the right for a 1. For example, given the bit sequence "10110101," begin with the top node and take the right branch. From there, take the left. Take the right from there, the right from there, and the left from there, and that was an "h." The following bits, "101," must be the beginning of another character.
The shortcoming of the incrementing technique used by PACKTEXT to determine unique codes now becomes apparent. It produces a severely imbalanced unpack tree. With only a few branches on the left of the root node, there are hundreds to the right. This means that the average number of nodes which must be visited to decode a character is higher than it could be, and, subsequently, it takes a little longer and uses a little more computer time to unpack than it might.
This unhappy nuance is balanced by the fact that the scarce branches to the left correspond to the most commonly used characters and are therefore more heavily traveled than the lengthier paths to the right. Regardless, the time required to traverse this tree for each character in the packed bitstream is easily overshadowed by the time required to read and write the disk files themselves.
 |
PROGRAM OPERATION
PACKTEXT is useful for compressing and restoring ASCII text files and possibly any data file in which data is stored by bytes. It would theoretically be of little use compressing files which aren't arranged by the byte, such as picture files. Nevertheless, for some reason, PACKTEXT seems able to compress most pictures, regardless of the theory which guided the program's inception. The DEGAS picture "COMET," a very nice medium-resolution picture on my copy of the distribution disk, is packed to 55% of its original size, including the custom 1K code table. The source listing for PACKTEXT, a file of the type the program was designed to handle is itself only packed to 68% of its original size. For that matter, the program file PACKTEXT.PRG, as random a collection of gibberish as any (although 25% zeroes) shrunk to 80% of its original size when presented to its own mercies. Strange how things work out, sometimes.
PACKTEXT can also be used for experimenting with Huffman Codes, and performing some character analysis on text files.
Packed files may or may not contain the Huffman Code Table which was used to pack them. You can analyze just one large representative text file and store the resulting code table for use with all text files. On the other hand, a user can analyze each file to be packed and store the code table used for that file along with the packed text itself. A more efficient packing would probably be achieved using the last method, but 1K will be lost to the table. You choose.
To create a file which is just a code table stored on disk for later use, select "Generate Huffman Codes" from the "Codes" menu. The program will prompt for the name of a text file to analyze. Once that process is finished, select "Save Huffman Codes" from the "File" menu. Once again, a name is prompted for. This creates a 1K file which you can reload for later use at any time.
To use such a code table, select "Load Huffman Codes" from the "File" menu; then select "Includes Codes in File," which will deactivate that item (which wakes up activated and checked in the menu). Now any file that is packed or unpacked will use that code table and will not include it in the packed file itself.
To pack files using tailored code tables, and this is the recommended method, first make certain "Include Codes in File" under the "File" menu is checked. Select "Pack a File" from under the "File" menu. PACKTEXT will prompt for the name of the file to be packed, and the name of a file to be created, then will build the code table and pack the file.
To unpack such a file, just select "Unpack a File" from the "File" menu. Whether or not "Include Codes in File" is checked, the code table from that file will be loaded and used to unpack it. Once again, the name of the packed file and a name for the newly created unpacked file will need to be entered.
Note: If a Huffman Code Table is stored in the packed file, the entire table (1K) is stored, not just the first part that contains the characters actually used. This would seem a waste since the entire object behind the program is to save disk space. It is nevertheless done this way because using a truncated code table on text, other than the specific text it applies to, can cause much grief if the other text includes characters not allowed for in the table. Since the code table from the packed file is retained until replaced by some other table, it's possible to do just that.
Source code is included, so anyone who wishes can fix this minor shortcoming. In doing so, the basic operation of the program will need to be changed somewhat.
PACKTEXT maintains three individual windows for display of interesting data and obtains all its instructions through a GEM menu bar. Available commands are:
- Analyze a text file to create a Huffman Code specially tailored for that file. ("Generate Huffman Codes").
- Print the Huffman Code Table currently in use. ("Print Huffman Codes").
- Pack a file. ("Pack a File").
- Unpack a file ("Unpack a File").
- Store the current Huffman Code Table in a file all by itself ("Save Huffman Codes").
- Retrieve a code table stored by the previous command. ("Load Huffman Codes").
- Open or close any of the three display windows. Some time savings is gained during packing and unpacking by closing the "Unpacked Text" window.
- Quit. Always handy in any program.
- A final menu option toggles whether or not the Huffman Code Table is stored along with the packed text in a packed file.
The Huffman Code Table currently in use, whatever its origin, is always displayed in the window entitled "Huffman Codes."
When a text file is packed or unpacked, the first MAXTEXT (=defined as 3000) characters of the unpacked file are displayed for your amusement in the window enticed "Unpacked Text."
The third window, entitled "Pack Data," contains statistics from pack and unpack operations. It shows the length of the unpacked text, in bytes, and the length of the packed data, also in bytes. In addition, the ratio of the length of the packed text to the unpacked text, labeled "packing efficiency," and the theoretical efficiency of the Huffman Code, labeled "efficiency rating," are displayed. This theoretical efficiency is the sum for each code (the product of its normalized frequency of occurrence and the length of its code in bits), all divided by eight; the number of bits in an unpacked ASCII character. The result is a ratio which, when multiplied by the size of an unpacked file gives the theoretical size of the corresponding packed file.
THE PROGRAM ITSELF
PACKTEXT's actual workings are left to the intrepid reader to wrestle from the included program listing. An exhaustive walkthrough exceeds the editorial space allotted for a single article. Nevertheless, for the impatient or unwilling, a few notes about the program's operation are in immediate order.
PACKTEXT allows the option of saving the Huffman Code Table itself along with the data in each packed file. Doing so increases the size of each by 1K but allows trouble-free use of customized code tables. The final result may well be a shorter file.
One can also store on disk by itself a single Huffman Code Table gleaned from an analysis of a single representative data file, storing only the data in each packed file. One can also simply use the default code table the program wakes up with, not storing any tables on disk.
With the "Include Codes in File" menu item checked, when the program is told to pack some data file, it will automatically analyze it, creating a customized code table before packing begins.
The "Generate Huffman Codes" menu item performs only the analysis, creating a customized code table for some data file. "Save. . " and "Load Huffman Codes" store and retrieve just the code table itself.
Also of interest is the precise meaning of the "efficiencies" the program is always calculating. "Efficiency rating" is the theoretical ratio of packed file size to unpacked file size, calculated from the frequency table and code lengths. "Packing efficiency" is in fact the actual ratio achieved during the last pack (or unpack). If a code table is retrieved from disk, the efficiency rating will be totally inaccurate because the frequency table isn't saved, in the interests of conserving space.
CONCLUSION
PACKTEXT is a versatile program that will certainly find use in some situations. Its most endearing social grace lies in the actual code used to compress and restore files. I hope the readers of START can use my examples to develop their own packing programs. How much can you squeeze down yourdata?